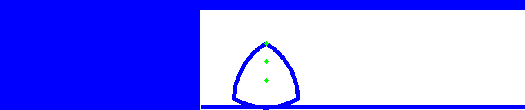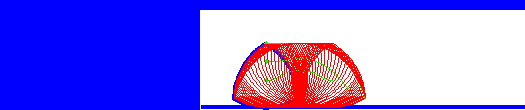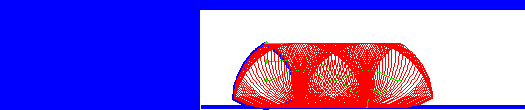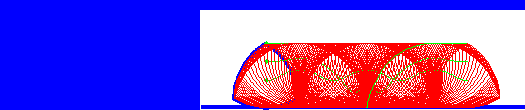
A Reuleaux triangle is the shape you get, starting from an equilateral triangle, and adding three circular arcs, drawn from each corner. It’s not actually a triangle, but what’s in a name?
The interesting thing is that a Reuleaux triangle is a shape of constant width. That means it can be used as a roller (but not a wheel). The animation below shows this – we can see that although the centre of the triangle moves up and down, the top surface of the rotating triangle is always level.
Follow the link below to see more, get links to 3D printable versions, and Matlab code to play with it.
It’s actually one of many shapes of constant width and the code here provides some matlab functions for creating these shapes, and manipulating them.
One of the trickiest things to do with such a triangle is that by rotating it around a non-fixed center, one can carve an approximate square, making a drill bit to drill a square hole (or nearly square) possible. The second animation shows this in action. However, you can see it doesn’t quite reach into the corners. We can improve on it with another shape of constant width generated by an Isosceles triangle. This time, we follow a curve generated from a point inside the triangle, but the beautiful thing is that it generates an exact square.
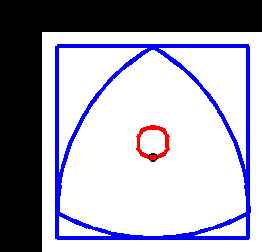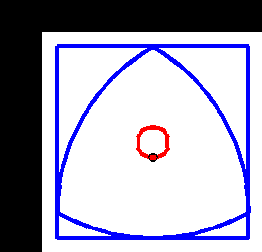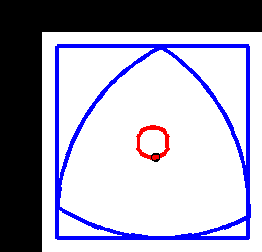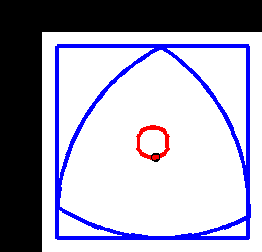
You can use your 3D printer to make one of these (at least to see the motion), using this. I have a pattern for the second one if anyone needs it too.
Using similar approaches, you can design other drill shapes. Have a look here to see a demo of a pentagonal drill 3D printed. Its a little sticky, but it works.
There’s more info in the zip file, along with examples of what you can do, including the animations.


